This post is by James, but Jason and I spent a lot of time talking about it. It’s important enough we needed lots of eyes.
I’m guessing that more than a few of the people who come to our site (or will come to our site, at any rate) think that we’re some kind of…what, institutional shills? Voices for Big Education, trying to force unneeded change down people’s throats? Heaven knows they’re out there.
Maybe I just want to think that’s how things are. It would actually be a compliment, in a strange kind of way. Proving we aren’t is partly why we mostly spend time on elementary examples and practical problems—it’s hard to claim propaganda when most readers can test the answers and ideas for themselves. We think that’s the best way to show that math education really can be improved.
On the other hand, the people who criticize changes in math education sometimes have a point. Sometimes, the changing standards really are used as an excuse for selling new textbooks, rather than making the textbooks better. And making tests, and testing systems, can be a great way to make money whenever state education rules change. They are a less effective way to make money (right now) if you actually have to improve them first.
And the only way to fight this kind of cheating, without giving up entirely, is to hold the folks who make the tests accountable. That’s today’s story. Before we go on, though, I’d like to say that while I am showing an example of a bad test, I also saw examples of good tests made by the same folks. There was a 4th-6th grade science test seemed particularly good, and the high-school level math test was also better than average. But somebody really messed up on the fifth-grade math test, and that’s bad timing if you want the kids to get to the good tests.
In this post, we are digging into specifics. That’s why I am writing specifically about the Utah state SAGE testing for math, grade 5, based on the sample problems taken from the official SAGE test portal. The science test I liked, as well as the high-school one that was decent, are also available there for free. I actually took this test myself, and then reviewed my answers with my brother, before writing this post.
The problems
The test starts with this:
That’s an OK start, I guess. I mean, it’s just a calculation problem, but it is the kind of problem that kids should be able to solve after grade 5. And we don’t want to start out too hard, do we?
Problem 2A is also OK, but not great. Once again, there is no real reason why we are adding six and eight, and then multiplying by three, but kids should know how to translate the words into the symbols, like the question asks. The user interface isn’t great, but it isn’t terrible in this particular problem.
Problem 2B, on the other hand, is, well, bad. What you are supposed to do is to rewrite (6+8)\times 3$ as 
Y’know what’s funny about this problem? I had completely forgotten what a rhombus was. (I think I mixed it up with a trapezoid, which also has four sides, but is defined very differently.) All these years using all kinds of fancy math, and I got tripped up, here, on the meaning of basic words. Luckily for students, the test includes a dictionary, so this is just me being kind of rusty.
That said, this is testing important skills in classification, geometry and logic. The truly important ideas—relationships between different type of objects—actually is pretty important in real math. So this is a decent question.
Finally, a word problem! It’s a pretty simple word problem, but at least its something. It’s also a multi-step problem, which is also an improvement. (You have to figure out how much money he actually spent, and then figure out how much more his estimate was than the actual amount he spent. You then have to turn it into an equation.)
Unfortunately, there’s a bit of a problem here, and it’s a pretty serious one.
Why are we turning this relationship into an equation?
I mean, seriously, why? It makes sense to say that the manager in the problem estimated way too high—ten times too high, in fact. (Or he overestimated the price by $4,500.) He obviously made an mistake in the multiplication. But—the equation doesn’t tell us anything about the situation that words wouldn’t, and just as well. The point of math is to communicate. This question is actually asking the student to make the result harder to understand for no reason at all. It looks like a word problem, but when you dig down to the real problem, the most important part is just math for math’s sake. A potentially useful skill, but it could be taught and tested in a much less—random—way.
If you want me to tell you when equations actually are useful, I will gladly tell you. It’s just, this isn’t one of them. The math they are testing is a poor fit for the simple word problem they created.
This question is pure mechanics. Anyone who wants to roll back math education standards should love it. I’m going to get more into this type of problem later, but for now I’ll say we probably want a few on the test, but it’s just OK, not good or great.
This is basically a good math problem, although a vague one. I’m actually glad that there is no single correct answer to this problem. (That’s true to how math works in the real world.) I just wish the question made it clearer to the student that they are just supposed to invent any two fractions which work. The problem should say that there is no one right answer, just right answers.
My far bigger complaint is about the way the problem is displayed. It wasn’t clear to me, on seeing the problem, that I was supposed to put one fraction in each box. When I first answered it, I put an addition problem in each box (providing two different answers to the question.) I suspect I would have gotten no credit for this problem, although I technically got it correct twice. This entire problem could have been solved by labeling the boxes more clearly, perhaps saying “Fraction 1” and “Fraction 2” to the left of the fraction boxes.
In fact, why bother with all the buttons and numbers on the bottom? Why force the students to use the fancy interface, when all they are really doing is typing in four numbers? Why not just have something like:
Find two fractions with different denominators which sum to
This is simpler and clearer and has a more natural way to enter the answers.
Reading geometric shapes is a useful skill in science/engineering/biology, etc. (Think of reading the plans for building a house. Or digging for oil. Or building a space probe.) So is being able to parse the logic in the true or false questions they ask the students. So on the whole, this question exercises good math skills that the students need to have.
On the other hand, we’re seven problems in and we still haven’t gotten a decent word problem in any of these questions. This kind of geometry is perfect for word problems—the world is full of these kinds of strange shapes, and it’s amazing when knowing things about them would be useful. It’s an OK problem, but it could have been so much more. More on this at the end.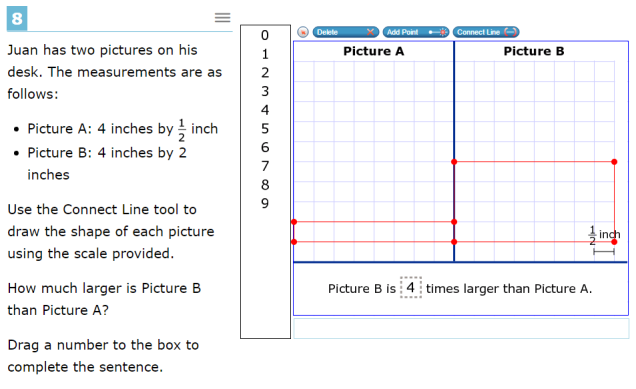 
This problem is bad. I do mean, very bad. It’s easily the worst sample problem on this whole test and shows off the worst of what has gone wrong with it. It’s not me, or even mostly me. When I showed Jason the first draft of my discussion of this problem, he thought I was being too nice. And he was right!
So what’s wrong with it? How may I count the ways?
- The “word problem” it’s attached to is probably the laziest excuse I have ever seen for a word problem. You could replace the first sentence with “Draw two rectangles,” and absolutely nothing else would change. There is no translating the word problem into math, or back again, the most important part of word problems. And the word problem as stated makes no sense. Who keeps a
inch picture of anything anywhere? It’s too narrow! And why are we drawing it on a graph, anyway? It’s a transparent attempt to say “Yeah, we got a word problem,” without doing any of the actual work to have a word problem.
- The way the user uses the machine to enter the answers is not how people normally use computers nowadays. It violates all the rules a student would have learned about doing graphics on a computer if they had used any other editing program anywhere. Jason says that his students found it very difficult to use. I certainly did.
- I have no idea how the computer grades this problem. As a professional programmer, my head hurts just thinking about all the correct answers a computer would mark wrong on this problem, because computers just aren’t that smart.
- What, exactly, is this problem supposed to be testing? The ability to draw rectangles? According to Jason, 5th grade is a bit late for that. It doesn’t match any of the known Utah Core standards. It doesn’t help students understand what a grid is supposed to stand for. What is the point, exactly?
Overall, a failure at about every level.
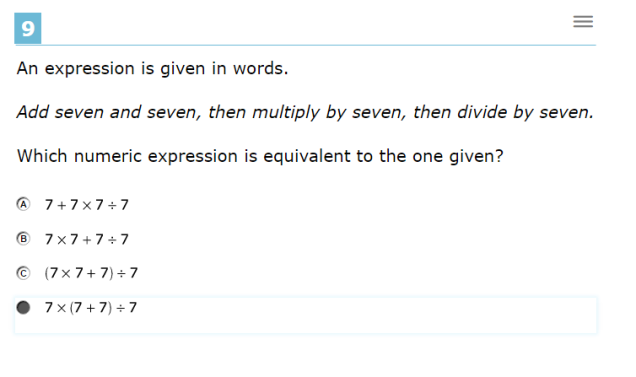
This is again an OK problem on its own, and actually does stick to the standard. I’ll discuss my main concern later as part of the wrap-up. Jason’s main concerns was two-fold: first, the problem uses only sevens, which can confuse the poor kids. This would have been a better problem with different numbers. Secondly, it’s not free-form enough for his taste. He thinks the problem would be better being split into two parts. In the first part, the kid tries to write down the expression given by the words, using their own symbols. Once they’ve done that, they can say which of the given expressions match their expression. In his experience, kids do a lot better job of learning the notation if they do it in that order.
Conclusions
Well, I was going to go on, but there’s no point. These work fine as a decent sample.
Many of you are probably wondering what was so bad about this test. After all, I said that many of the problems were OK. And that’s just the problem:
This test is mediocre at best. All together, it is actually pretty bad.
Some of the problems are OK on their own. All of them (except problem 8) could have a place inside a good test. But taken together, they are just traditional math problems! Pointless, mechanical math problems. You need to test mechanics on a math test, but word problems do a perfectly good job of testing mechanics.
And there is the problem right there. There are no good word problems on this test. None! None of these problems have an interesting motivation or story-line. For instance, problem 1 could be replaced with the question:
“If a rectanglular kitchen has one side that is 68ft long and the other is 90ft long, how many 1ft by 1ft tiles will you need to cover the whole floor?”
The math problem the student has to solve exactly the same as in the original version. Translating the problem into math, and then back out, may be harder than the original problem, but it is necessary for students to have this skill anyway. The entire test could have been brought up a notch just by choosing better word problems. Not for every problem should be a word problem (mechanics really is important) but it should have happened much more often than it did.
And that’s not even as good as it could get. It could get much better. Go check out the fifth grade science SAGE practice test—that test is a whole lot better. On that test, you get to do virtual experiments with rocks, comparing their hardness, how they react with acid, and similar things. You use the result of one problem to feed into the next problem. The whole thing just feels more-real.
You can do exactly the same thing with math. With math, you can set up interesting scenarios which need math to solve. You can have one problem feed into the next. You can ask the students what the answers to specific problems mean. That’s how science and engineering and business actually use math in the real world! And this test did nothing to live up to this kind of standard. Argh! Frustrating! The high school level SAGE test was a lot better-it used more word problems for one-but even it could be seriously improved by being treated more like science—more like math is actually used.
And remember: math was made to be used.
The Math Dragons 